How is it possible for us to communicate securely when there’s the possibility of a third party eavesdropping on us? How can we communicate private secrets through public channels? How do such techniques enable us to bank online and carry out other sensitive transactions on the Internet while trusting numerous relays? In this post, I hope to explain public key cryptography, with actual code examples, so that the concepts are a little more concrete.

First, please check out this excellent video on public key crypto:

{% youtube YEBfamv-_do %}

Hopefully that explains the gist of the technique, but what might it actually look like in code? Let’s take a look at example code in JavaScript using the Node.js crypto module. We’ll later compare the upcoming WebCrypto API and look at a TLS handshake.

Meet Alice. Meet Bob. Meet Eve. Alice would like to send Bob a secret message. Alice would not like Eve to view the message. Assume Eve can intercept, but not tamper with, everything Alice and Bob try to share with each other.

Alice chooses a modular exponential key group, such as modp4, then creates a public and private key.

var group = "modp4";
var aliceDH = crypto.getDiffieHellman(group);
aliceDH.generateKeys();

A modular exponential key group is simply a “sufficiently large” prime number, paired with a generator (specific number), such as those defined in RFC2412 and RFC3526.

The public key is meant to be shared; it is ok for Eve to know the public key. The private key must not ever be shared, even with the person communicating to.

Alice then shares her public key and group with Bob.

Public Key:
 <Buffer 96 33 c5 9e b9 07 3e f2 ec 56 6d f4 1a b4 f8 4c 77 e6 5f a0 93 cf 32 d3 22 42 c8 b4 7b 2b 1f a9 55 86 05 a4 60 17 ae f9 ee bf b3 c9 05 a9 31 31 94 0f ... >
Group: 
 modp14

Bob now creates a public and private key pair with the same group as Alice.

var bobDH = crypto.getDiffieHellman(group);
bobDH.generateKeys();

Bob shares his public key with Alice.

Public key:
 <Buffer ee d7 e2 00 e5 82 11 eb 67 ab 50 20 30 81 b1 74 7a 51 0d 7e 2a de b7 df db cf ac 57 de a4 f0 bd bc b5 7e ea df b0 3b c3 3a e2 fa 0e ed 22 90 31 01 67 ... >

Alice and Bob now compute a shared secret.

var aliceSecret = aliceDH.computeSecret(bobDH.getPublicKey(), null, "hex");
var bobSecret = bobDH.computeSecret(aliceDH.getPublicKey(), null, "hex");

Alice and Bob have now derived a shared secret from each others’ public keys.

aliceSecret === bobSecret; // => true

Meanwhile, Eve has intercepted Alice and Bob’s public keys and group. Eve tries to compute the same secret.

var eveDH = crypto.getDiffieHellman(group);
eveDH.generateKeys();
var eveSecret = eveDH.computeSecret(aliceDH.getPublicKeys(), null, "hex");

eveSecret === aliceSecret; // => false

This is because Alice’s secret is derived from Alice and Bob’s private keys, which Eve does not have. Eve may not realize her secret is not the same as Alice and Bob’s until later.

That was asymmetric encryption; using different keys. The shared secret may now be used in symmetric encryption; using the same keys.

Alice creates a symmetric block cypher using her favorite algorithm, a hash of their secret as a key, and random bytes as an initialization vector.

var cypher = "aes-256-ctr";
var hash = "sha256";
var aliceIV = crypto.randomBytes(128);
var aliceHashedSecret = crypto.createHash(hash).update(aliceSecret).digest("binary");
var aliceCypher = crypto.createCypher(cypher, aliceHashedSecret, aliceIV);

Alice then uses her cypher to encrypt her message to Bob.

var cypherText = aliceCypher.update("...");

Alice then sends the cypher text, cypher, and hash to Bob.

cypherText:
 <Buffer bd 29 96 83 fa a8 7d 9c ea 90 ab>
cypher:
 aes-256-ctr
hash:
 sha256

Bob now constructs a symmetric block cypher using the algorithm from Alice, and a hash of their shared secret.

var bobHashedSecret = crypto.createHash(hash).update(bobSecret).digest("binary");
var bobCypher = crypto.createDecipher(cypher, bobHashedSecret);

Bob now decyphers the encrypted message (cypher text) from Alice.

var plainText = bobCypher.update(cypherText);
console.log(plainText); // => "I love you"

Eve has intercepted the cypher text, cypher, hash, and tries to decrypt it.

var eveHashedSecret = crypto.createHash(hash).update(eveSecret).digest("binary");
var eveCypher = crypto.createDecipher(cypher, eveHashedSecret);
console.log(eveCypher.update(cypherText).toString());

// => ��_r](�i)

Here’s where Eve realizes her secret is not correct.

This prevents passive eavesdropping, but not active man-in-the-middle (MITM) attacks. For example, how does Alice know that the messages she was supposedly receiving from Bob actually came from Bob, not Eve posing as Bob?

Today, we use a system of certificates to provide authentication. This system certainly has its flaws, but it is what we use today. This is more advanced topic that won’t be covered here. Trust is a funny thing.

What’s interesting to note is that the prime and generator used to generate Diffie-Hellman public and private keys have strings that represent the corresponding modular key exponential groups, ie “modp14”. Web crypto’s API gives you finer grain control to specify the generator and large prime number in a Typed Array. I’m not sure why this is; if it allows you to have finer grain control, or allows you to support newer groups before the implementation does? To me, it seems like a source for errors to be made; hopefully someone will make a library to provide these prime/generator pairs.

One issue with my approach is that I assumed that Alice and Bob both had support for the same hashing algorithms, modular exponential key group, and symmetric block cypher. In the real world, this is not always the case. Instead, it is much more common for the client to broadcast publicly all of the algorithms it supports, and the server to pick one. This list of algorithms is called a “suite,” ie “cypher suit.” I learned this the hard way recently trying to upgrade the cypher suit on my ssh server and finding out that my client did not support the lastest cyphers. In this case, Alice and Bob might not have the same versions of Node.js, which statically link their own versions of OpenSSL. Thus, one should use cryto.getCiphers() and crypto.getHashes() before assuming the party they’re communicating to can do the math to decrypt. We’ll see “cypher suites” come up again in TLS handshakes. The NSA publishes a list of endorsed cryptographic components, for what it’s worth. There are also neat tricks we can do to prevent the message from being decrypted at a later time should the private key be compromised and encrytped message recorded, called Perfect Forward Secrecy.

Let’s take a look now at how a browser does a TLS handshake. Here’s a capture from Wireshark of me navigating to https://google.com. First we have a TLSv1.2 Client Hello to start the handshake. Here we can see a list of the cypher suites.

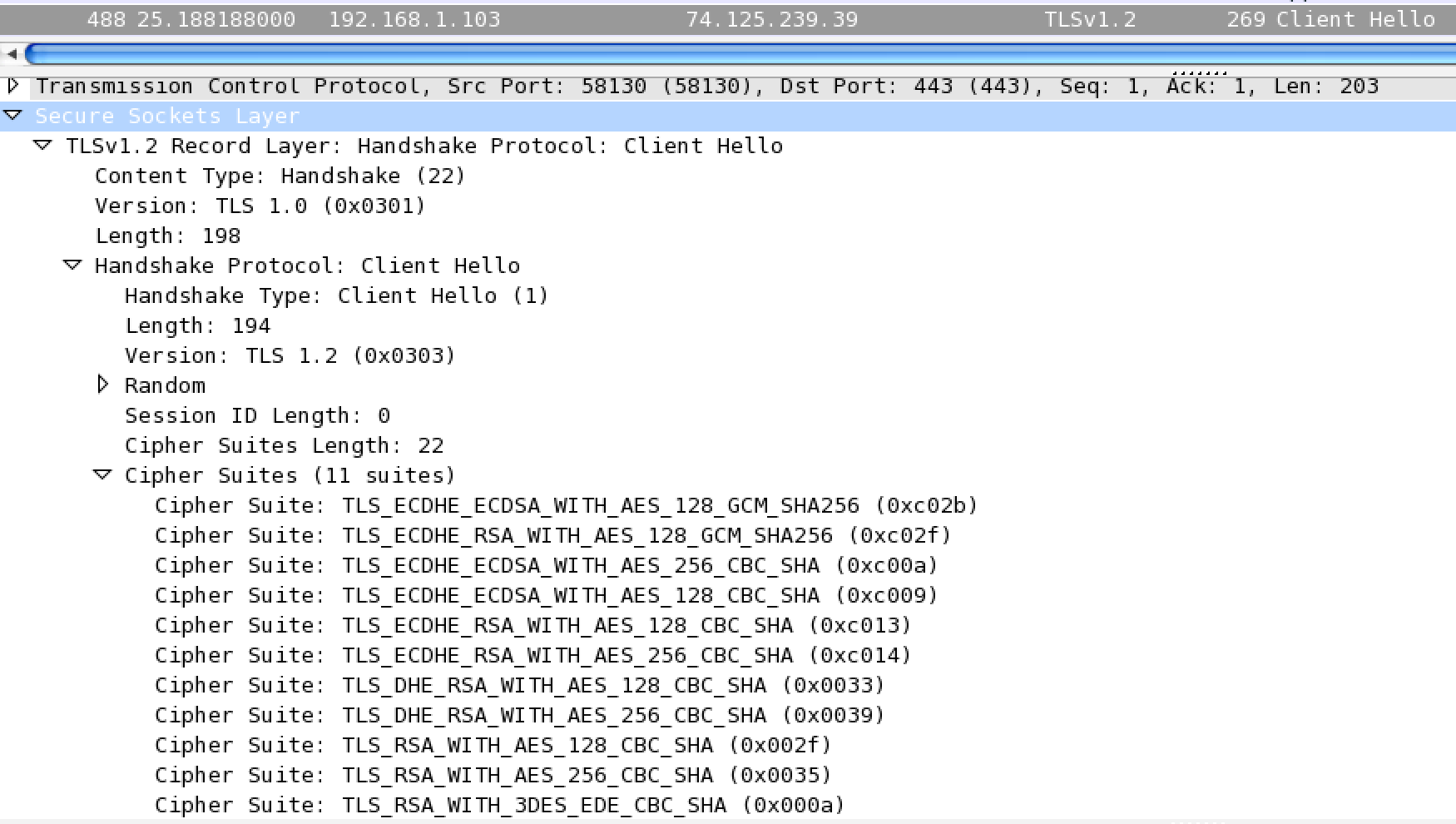
Next is the response from the server, a TLSv1.2 Server Hello. Here you can see the server has picked a cypher to use.

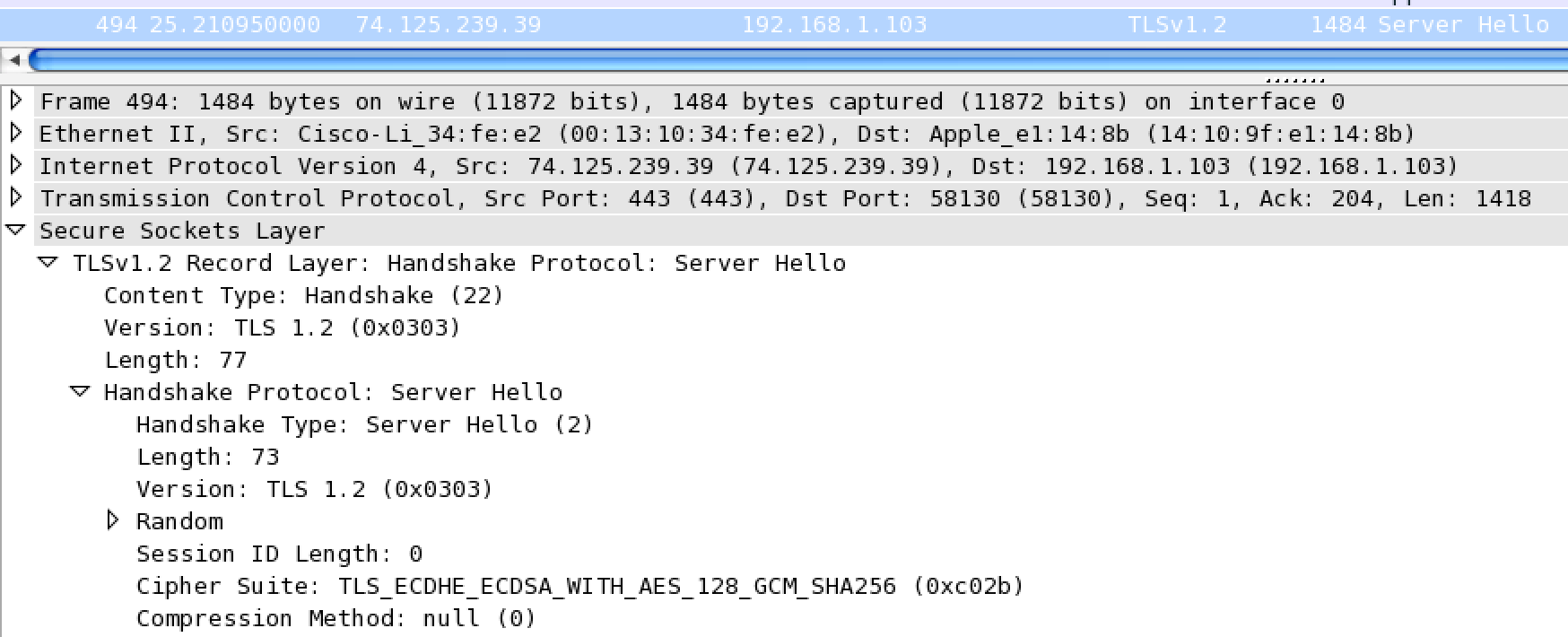
The server then sends its certificate, which contains a copy of its public key.

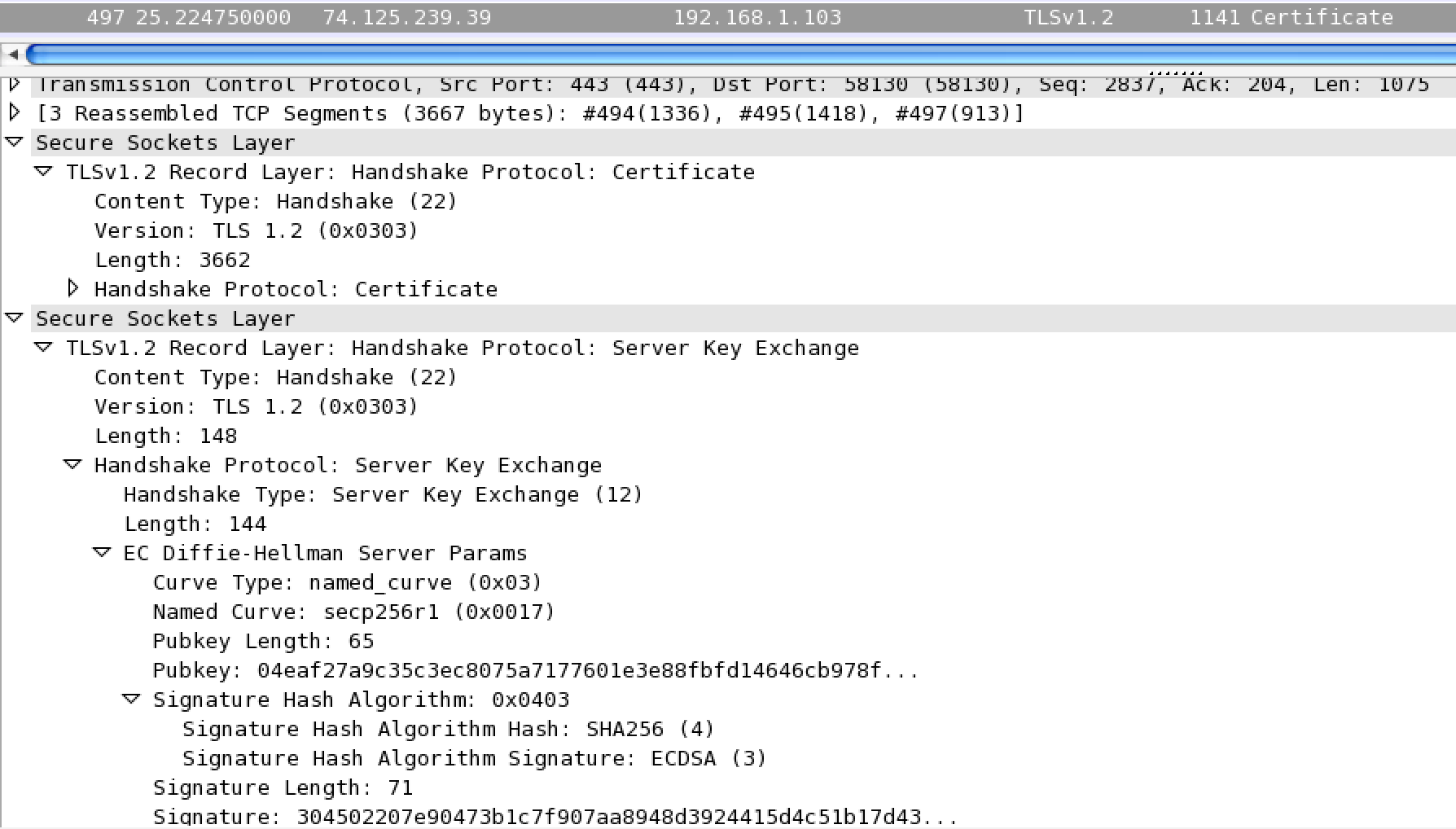
Now that we’ve agreed on a cypher suite, the client now sends its public key. The server sets up a session, that way it may abbreviate the handshake in the future. Finally, the client may now start making requests to the server with encrypted application data.

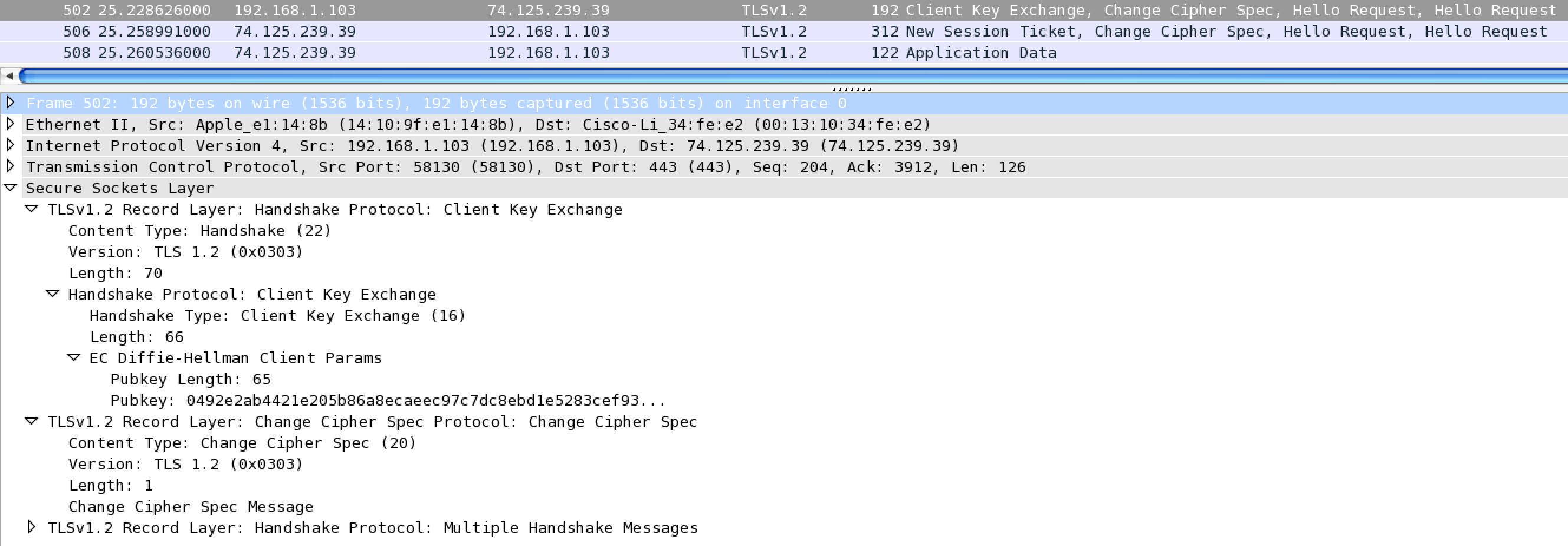
For more information on TLS handshakes, you should read Ilya Grigorik’s High Performance Browser Networking book chapter TLS Handshake, Mozilla OpSec’s fantastic wiki, and this exellent Stack Exchange post. As you might imagine, all of these back and forth trips made during the TLS handshake add latency overhead when compared to unencrypted HTTP requests.

I hope this post helped you understand how we can use cryptography to exchange secret information through public channels. This isn’t enough information to implement a perfectly secure system; end to end security means one single mistake can compromise the entire system. Peer review and open source, battle tested implementations go a long way.

A cryptosystem should be secure even if everything about the system, except the key, is public knowledge.

I wanted to write this post because I believe abstinence-only crypto education isn’t working and I cant stand when anyone acts like part of a cabal from their ivory tower to those trying to learn new things. Someone will surely cite Javascript Cryptography Considered Harmful, which while valid, misses my point of simply trying to show people more concrete basics with code examples. The first crypto system you implement will have its holes, but you can’t go from ignorance of crypto to perfect knowledge without implementing a few imperfect systems. Don’t be afraid to, just don’t start with trying to protect high value data. Crypto is dangerous, because it can be difficult to impossible to tell when your system fails. Assembly is also akin to juggling knives, but at least you’ll usually segfault if you mess up and program execution will halt.

With upcoming APIs like Service Workers requiring TLS, protocols like HTTP2, pushes for all web traffic to be encrypted, and shitty things governments, politicians, and ISPs do, web developers are going to have to start boning up on their crypto knowledge.

What are your recommendations for correctly learning crypto? Leave me some thoughts in the comments below.